
Lexikon
Lexikon

Hier sind die Fachbegriffe, die Ihnen bei den Themen Wärmeschutz und Feuchteschutz am Gebäude begegnen, übersichtlich zusammengefasst.
Im Lexikon finden sich die wichtigsten Kenngrößen für den baulichen Wärmeschutz auf einen Blick. Kenngrößen für Wärme- und Energiebedarf und Wärmeverluste sowie Kenngrößen die den Energietransport oder Temperaturverhältnisse beschreiben.
Der Jahres-Heizwärmebedarf eines Gebäudes beschreibt die theoretisch berechnete Energie, die notwendig ist, um ein Gebäude zu beheizen. Nicht beinhaltet sind dabei die Verluste der Anlagentechnik sowie die Verluste bei Energiegewinnung und Transport (siehe Abbildung unten).
Damit wird deutlich, dass es sich hierbei um eine Größe handelt, die nur einen sehr kleinen Ereignisrahmen betrachtet.
Berechnung des Jahres-Heizwärmebedarfs
Qh = 66 ⋅ ( HT + Hv) - 95 ⋅ ( Qs + Qi )
- HT: Spezifischer Transmissionswärmeverlust
- Hv: Spezifischer Lüftungswärmeverlust
- Qs: Solare Gewinne
- Qi: Interne Gewinne
Bei der Berechnung des Jahres-Heizwärmebedarfs werden die Wärmeverluste durch alle Bauteile (Transmissionswärmeverluste) und durch Lüftung berücksichtigt. Dem werden die Wärmegewinne durch Sonneneinstrahlung und interne Gewinne (z.B. durch elektrische Geräte) werden wie eine Art Gutschrift davon abgezogen.
Der Jahres-Primärenergiebedarf beschreibt den Energiebedarf von der Herstellung bzw. Gewinnung der Energiequelle über den Transport bis hin zum Verbrauch. Damit werden regenerative Energiequellen, eine effiziente Anlagentechnik und ein hoher Wärmedämmstandard positiv berücksichtigt.
Folglich betrachtet der Primärenergiebedarf den „tatsächlichen" Energieverbrauch und bietet somit eine sehr umfassende Vergleichs- und Bewertungsmöglichkeit.
Berechnung des Jahres-Primärenergiebedarfs
(vereinfachter Ansatz für Wohngebäude)
QP = ( Qh + Qw ) ⋅ eP
- Qh: Jahres-Heizwärmebedarf
- Qw: Jahres-Wärmebedarf für Warmwasser
- eP: Anlagenaufwandszahl
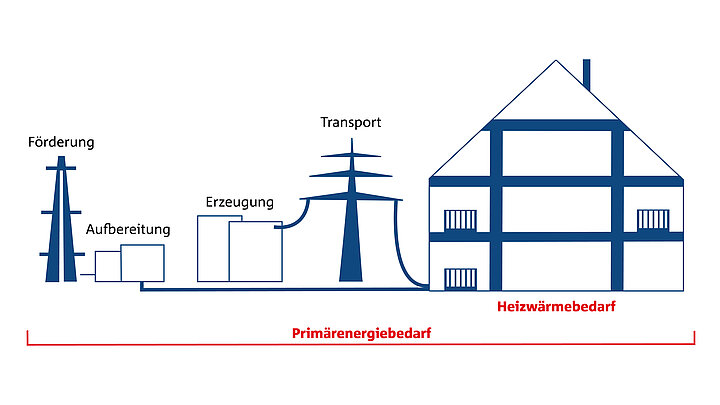
Darstellung zur Abgrenzung von Primärenergiebedarf zu Heizwärmebedarf: Der Heizwärmebedarf definiert den berechneten Energieverbrauch im Gebäude der ab der Heizungsanlage zur Beheizung der Räume aufgewendet wird., während der Primärenergiebedarf zusätzlich die Energiebeschaffung, den Transport und die Qualität der Heizungsanlage beinhaltet.
Transmissionswärmeverlust HT
Der Transmissionwärmeverlust beschreibt die Wärmeenergieverluste, die durch die Gebäudehülle abgegeben werden. In der DIN V 18599 wird er als Transmissionswärmetransferkoeffizient bezeichnet.
Zur Ermittlung der Transmissionswärmeverluste werden die energetischen Verluste durch die einzelnen flächigen Bauteile des Gebäudes sowie die Energieverluste durch Wärmebrücken summiert. Die Transmissionswärmeverluste durch flächige Bauteile werden durch den U-Wert des Bauteils pro Fassadenfläche des Bauteils (Formelzeichen A) berechnet. Je nach Situation werden die Verluste der Bauteile noch mit einem Temperaturkorrekturfaktor (FX-Wert) korrigiert. Die Transmissionswärmeverluste durch Wärmebrücken HWB können entsprechend der drei folgenden Möglichkeiten ermittelt werden. Eine ausführliche Beschreibung findet sich unter GEG Wärmebrücken-Nachweis.
Berechnung des Transmissionswärmeverlustes
HT = ∑( Fxi ⋅ Ui ⋅ Ai ) + HWB
Für den Wärmeverlust über Wärmebrücken gibt es verschiedene Möglichkeiten der Ausführung und Berechnung:
1. Pauschale Methode (Standard)
HWB = ΔUWB ⋅ ∑Ai mit ΔUWB = 0,10 W/(m2K)
2. Pauschale Methode (Verbessert)
HWB = ΔUWB ⋅ ∑Ai mit ΔUWB = 0,05 W/(m2K) bzw. 0,03 W/(m2K)
Dieser Ansatz ist nur zulässig, wenn die Wärmebrücken entsprechend Beiblatt 2 zu DIN 4108 ausgebildet sind (Kategorie A bzw. B).
3. Detaillierte Methode
HWB = ∑Fj ⋅ ψj ⋅ Ij + ∑Fk ⋅ χk
Dieser Ansatz ist nur zulässig, wenn Wärmebrückendetails nachgewiesen werden, durch Angaben in Wärmebrückenkatalogen oder durch FE-Berechnungen.
Begriffsdefinitionen zu den Formeln:
- HWB ist der Anteil des Wärmebrückeneinflusses an HT
∑Fj ⋅ Ui ⋅ Ai
beschreibt den Wärmeverlust über alle flächigen Bauteile (Wände, Decken, Fenster etc.) mit Ui als Wärmedurchgangskoeffizient der Wand i mit der außenmaßbezogenen Fläche Ai und dem Temperatur-Reduktionsfaktor Fi.
∑Fj ⋅ ψj ⋅ Ij
stellt den zusätzlichen Wärmeverlust über alle linienförmigen Wärmebrücken (z. B. Balkone, Mauerfuß am Gebäudesockel) dar, mit ψj als außenmaßbezogener, längenbezogener Wärmedurchgangskoeffizient der linienförmigen Wärmebrücke j mit der Länge lj und dem Temperatur-Reduktionsfaktor Fj.
∑Fk ⋅ χk
stellt den zusätzlichen Wärmeverlust über alle punktförmigen Wärmebrücken (z. B. Durchdringung der Außenwand durch Stahlträger) dar, mit χk als punktförmiger Wärmedurchgangskoeffizient der punktförmigen Wärmebrücke k und dem Temperatur-Reduktionsfaktor Fk.
Spezifischer Transmissionswärmeverlust H‘T
Mit H‘T (gesprochen: „H Strich T“ oder „H T Strich“) wird der spezifische, auf die wärmeübertragende Umfassungsfläche bezogene Transmissionswärmeverlust der Außenbauteile bezeichnet. Auf dessen Basis wird im Gebäudeenergiegesetz die Anforderung an die Dämmqualität der Gebäudehülle als Ganzes festgesetzt. Da der H‘T der Transmissionswärmeverlust bezogen auf die gesamte Gebäudehüllfläche ist (Einheit: W/(m²K)), wird er auch mittlerer U-Wert genannt.
Wenn durch Sonneneinstrahlung der Wohnraum aufgeheizt wird, spricht man von solaren Wärmegewinnen. Während diese im Winter als Unterstützung der Heizung durchaus erwünscht sind, können sie in den Übergangszeiten oder im Sommer leicht zu einer Überhitzung des jeweiligen Raumes führen. Die Erwärmung … kann durch das Aufheizen von opaken Bauteilen oder durch direkte Transmission (Durchgang) der Wärmestrahlung durch Fenster verursacht werden.
Als sommerlicher Wärmeschutz werden die Maßnahmen bezeichnet, die den Wärmeeintrag durch Sonnenstrahlung reduzieren. Dies wird vorzugsweise durch Verschattungsmaßnahmen umgesetzt. Dies kann durch auskragende Bauteile wie Balkone aber auch durch Rollläden, Markisen u. ä. ausgeführt werden. Die Einhaltung des sommerlichen Wärmeschutzes wird im GEG gefordert und wird in der DIN 4108 geregelt.
Dabei werden Anforderungen an Abmessungen und Ausrichtungswinkel der Fenster, an Verglasungsart, Maßnahmen zur Verschattung und weitere Einflussgrößen wie beispielsweise dem Lüftungsverhalten der Nutzer gestellt. Auch die Bauart des Gebäudes (schwer, mittel, leicht) wird berücksichtigt. Neben dem vereinfachten Nachweis ist auch derjenige durch thermische Gebäudesimulation möglich (vgl. DIN 4108-2, Abschnitt 8).
Der WärmestromФ (gesprochen: phi, Einheit: Watt) beschreibt den Wärmetransport von Wärmeenergie (Einheit: Joule) abhängig von der Zeit (Einheit: s). Der Wärmetransport wird durch die temperaturabhängige Eigenbewegung von Atomen und Molekülen verursacht. Dabei ist die Fließrichtung des Wärmestroms per Definition von einem Bereich höherer hin zu einem Bereich niedriger Temperatur.
Die Wärmeleitfähigkeit λ (gesprochen: lambda) beschreibt, wieviel Wärme durch ein Material dringt. Dabei bedeutet ein kleiner λ-Wert eine niedrige Wärmeleitfähigkeit bzw. einen hohen Wärmewiderstand und damit gute Wärmedämmung. So hat Stahl beispielsweise eine sehr hohe Wärmeleitfähigkeit (15 bis 50 W/(mK)), während Dämmung eine sehr niedrige Wärmeleitfähigkeit aufweist (ca. 0,035 W/(m∙K)).
In der Theorie wird die Wärmemenge in Ws gemessen, die in 1 s durch 1 m² einer 1 m dicken homogenen Stoffschicht senkrecht zu den Oberflächen fließt, wenn der Temperaturunterschied 1 K beträgt. Es wird von 10 °C zu 9 °C gemessen. In der Praxis hat der Probenkörper kleinere Abmessungen und das Ergebnis wird entsprechend umgerechnet.
Die äquivalente Wärmeleitfähigkeit λeq
Die äquivalente Wärmeleitfähigkeit λeq eines aus mehreren Baumaterialien bestehenden Bauelementes ist die Wärmeleitfähigkeit eines homogenen, quaderförmigen Ersatzbaustoffes gleicher Außenabmessung, welcher anstelle des komplexen Bauelementes im eingebauten Zustand die gleiche wärmeschutztechnische Wirkung erzielt.
Gemäß dem Europäischen Bewertungsdokument (European Assessment Document - EAD) für tragende Wärmedämmelemente, das 2017 eingeführt wurde, wird λeq wie folgt ermittelt:
Bei der Berechnungsmethode nach EAD wird eine detaillierte dreidimensionale Wärmebrückenberechnung mit dem tragenden Wärmedämmelement durchgeführt. Dabei werden allerdings die angrenzenden Bauteile auf beiden Seiten auf 30 mm Breite begrenzt. Dabei wird der komplexe Aufbau eines tragenden Wärmedämmelements wird im Detail modelliert und der Wärmeverlust über die Wärmebrücke bestimmt. Aus dem auftretenden Wärmeverlust werden die äquivalente Wärmeleitfähigkeit λeq und der äquivalente Wärmedurchlasswiderstand Req ermittelt.
Die detaillierte Wärmebrückenberechnung
Soll ein detaillierter Wärmebrückennachweis zur Ermittlung von ψ- oder fRsi-Werten geführt werden, kann für die Modellierung des Anschlussdetails der λeq-Wert verwendet werden. Dafür wird ein homogenes Rechteck mit den Abmessungen des Dämmkörpers des Schöck Isokorb® an dessen Position im Modell gesetzt und diesem die äquivalente Wärmeleitfähigkeit λeq zugewiesen (siehe Abbildung unten). So können bauphysikalische Kennwerte einer gesamten Konstruktion auf einfache Weise errechnet werden.
Die Berechnungsmethodik zur Ermittlung von λeq wurde auf Grundlage des Europäischen Bewertungsdokuments (European Assessment Document - EAD) für tragende Wärmedämmelemente und darauf aufbauend für den Schöck Isokorb® in der europäischen technischen Bewertung (European Technical Assessment - ETA) validiert.
Mit marktüblicher Wärmebrücken-Software kann mithilfe der thermischen Randbedingungen nach DIN EN ISO 6946 sowie DIN 4108 Beiblatt 2 eine Berechnung erfolgen. Damit können neben den Wärmeverlusten der Wärmebrücke (ψ-Wert) auch die Oberflächentemperaturen ϴsi und damit auch der Temperaturfaktor fRsi berechnet werden.
Die einzelnen λeq-Werte finden Sie in „Technische Information > Bauphysikalische Kennwerte“.
Der Wärmedurchlasswiderstand ist der Widerstand, den ein Material dem Wärmestrom bei 1K (Kelvin) Temperaturdifferenz auf der Fläche von einem m² entgegensetzt.
Berechnet wird R als Dicke des Materials geteilt durch seine Wärmeleitfähigkeit:
λ: Wärmeleitfähigkeit in W/(m∙K)
d: Materialdicke in m
Diese Berechnung eines R-Werts kann auch für ein mehrschichtiges Bauteil durchgeführt werden:
Werden zusätzlich die Wärmeübergangswiderstände an den Oberflächen (Luft zu Bauteil und Bauteil zu Luft) hinzu addiert, erhält man den sogenannten Wärmedurchgangswiderstand.
Der Wärmedurchgangskoeffizient beschreibt den Wärmedurchgang durch ein Bauteil. Er beruht auf dem R-Wert eines Bauteils und beinhaltet zusätzlich die Wärmeübergangswiderstände der an das Bauteil angrenzenden Luftschichten (Rsi für innen und Rse für außen). Er ist der Kehrwert vom Wärmedurchgangswiderstand. Damit stellt der U-Wert den tatsächlichen Wärmedurchgang von Raumluft zu Raumluft bzw. Raumluft zur Außenluft dar.
Berechnet wird der U-Wert als Kehrwert der Summe des gesamten Wärmedurchlasswiderstandes und der beiden Wärmeübergangswiderstände:

Der thermische Leitwert ist der Quotient aus dem Wärmestrom je Meter Länge einer linienförmigen Wärmebrücke und der Temperaturdifferenz zwischen zwei Räumen, die durch die betrachtete Konstruktion getrennt sind. Somit stellt der Leitwert die Wärmeverluste durch diese Konstruktion dar.
Formel aus DIN EN ISO 10211:
Für eine Konstruktion mit Wärmebrücken setzt sich der dreidimensionale thermische Leitwert L3D aus den flächigen Transmissionswärmeverlusten durch die ungestörten Bauteile und aus den Transmissionswärmeverlusten durch die Summe aller Wärmebrücken zusammen, wie in der folgenden Formel (nach DIN EN ISO 10211) dargestellt:
Formel aus DIN EN ISO 10211:
Dabei ist:
- Uk(i,j) der Wärmedurchgangskoeffizient von Teil k des Raums oder Gebäudes;
- Ak die Fläche, für die der Wert Uk(i,j) gilt;
- Ψm(i,j) der lineare Wärmedurchgangskoeffizient von Teil m des Raums oder Gebäudes;
- lm die Länge, über die der Wert Ψm(i,j) gilt;
- χn(i,j) der punktbezogene Wärmedurchgangskoefizient von Teil n des Raums oder Gebäudes;
- Nk die Anzahl der Wärmedurchgangskoeffizienten;
- Nm die Anzahl der längenbezogenen Wärmedurchgangskoeffizienten;
- Nn die Anzahl der punktbezogenen Wärmedurchgangskoeffizienten.
Bei Transmissionswärmeverlusten an Wärmebrücken wird unterschieden, ob es sich um eine linienförmige Wärmebrücke (z.B. ein Balkonanschluss) oder eine punktuelle Wärmebrücke (z.B. Anker in der Fassade) handelt.
Der längenbezogene Wärmedurchgangskoeffizient ψ (Einheit: W/(m∙K), gesprochen psi) kennzeichnet den pro lfm. zusätzlich auftretenden Wärmeverlust einer linienförmigen Wärmebrücke. Der punktbezogene Wärmedurchgangskoeffizient χ (Einheit: W/K, gesprochen chi) kennzeichnet entsprechend den zusätzlichen Wärmeverlust über eine punktförmige Wärmebrücke.
Der ψ -Wert ist von der Konstruktionsqualität, den Abmessungen und den U-Werten der anschließenden Bauteile abhängig. Das ist so, weil die Wärmebrücke und die angrenzende Konstruktion sich gegenseitig bzgl. des Wärmestromverlaufs beeinflussen. Damit ändert sich der ψ-Wert, wenn sich die angrenzende Konstruktion ändert, selbst wenn die Wärmebrücke an sich gleich bleibt.
In der Abbildung ist zu sehen, wie der ψ-Wert für eine ungestört durch die Wand durchlaufende Balkonplatte aussieht. Dieser zusätzliche Wärmeverlust durch die Balkonplatte beeinflusst auch die angrenzende Wand. Praktisch bedeutet das, dass durch den Abfluss der Wärme über die Balkonplatte auch die Wand oberhalb und unterhalb der Wärmebrücke auskühlt. An den Pfeilen ist zu sehen, welchen Weg die Wärmeströme dabei nehmen. Während bei ungestörten Wänden nur horizontale Warmeströme auftreten (ober- und unterhalb der Betonplatte), sind die Warmeströme in Wärmebrücken (im Bereich der Betonplatte). Hieraus wird ersichtlich, warum die Ermittlung von ψ-Werten wesentlich komplexer ist als die von U-Werten.
Auszug aus DIN EN ISO 10211:
Berechnung der längen- und punktbezogenen Wärmedurchgangskoeffizienten
Die ψ-Werte werden bestimmt nach:
Dabei ist:
- L2D der thermische Leitwert aus einer 2D-Berechnung des die beiden betrachteten Räume trennenden Bauteils;
- Uj der Wärmedurchgangskoeffizient des die beiden betrachteten Räume trennenden 1D-Bauteils j;
- lj die Länge, für die der Wert Uj gilt.
Die χ-Werte werden bestimmt nach:
Dabei ist:
- L3D der thermische Leitwert aus einer 3D-Berechnung;
- Ui der Wärmedurchgangskoeffizient des die beiden betrachteten Räume trennenden 1D-Bauteils;
- Ai die Fläche, über die der Ui-Wert gilt;
- ψi der längenbezogene Wärmedurchgangskoeffizient;
- lj die Länge, über die der ψi-Wert gilt;
- Ni die Anzahl der 1D-Bauteile;
- Nj die Anzahl der 2D-Bauteile.
Längenbezogener Wärmedurchgangskoeffizient (Definition aus DIN EN ISO 10211):
Quotient aus Wärmestrom im stationären Zustand und dem Produkt aus Länge und Temperaturdifferenz zwischen den Umgebungstemperaturen auf jeder Seite der Wärmebrücke.
Punktbezogener Wärmedurchgangskoeffizient (Definition aus DIN EN ISO 10211):
Quotient aus Wärmestrom im stationären Zustand und der Temperaturdifferenz zwischen den Umgebungstemperaturen auf jeder Seite der Wärmebrücke.
Taupunkttemperatur θτ
Die Taupunkttemperatur θτ ist diejenige Temperatur, bei der die in der Raumluft vorhandene Feuchtigkeit nicht mehr von der Raumluft gehalten werden kann und dann in Form von Wassertröpfchen abgegeben wird. Die relative Raumluftfeuchte beträgt dann 100 %.
Schimmelpilztemperatur θs
An kalten Bauteiloberflächen besteht dann ein deutlich erhöhtes Schimmelpilzrisiko, wenn die Bauteiloberfläche so kalt ist, dass sich in der direkt anliegenden Luftschicht eine relative Feuchte von 80 % einstellt. Die Temperatur, bei der diese Situation eintritt, ist die sogenannte Schimmelpilztemperatur θS. Ist die Temperatur noch niedriger und somit die relative Feuchte an der entsprechenden Stelle höher, nimmt das Schimmelpilzrisiko weiter zu.





